设函数f(x)=(x-a)(x-b)(x-c),a,b,c属于R,f'(x)为f(x)的导函数。
(1)若a=b=c,f(4)=8,求a的值;
(2)若a≠b,b=c,且f(x)和f'(x)的零点均在集合{-3,1,3}中,求f(x)的极小值;
(3)若a=0,0<b≤1,c=1,且f(x)的极大值为M,求证:M≤4/25。
解析:
(1)第一小题纯粹送分,直接带就行
f(x)=(x-a)3
f(4)=(4-a)3
a=2
(2)第二题老规矩,把未知数尽量减少
这里我把f(x)里所有的c换成b
f(x)=(x-a)(x-b)2到了这一步,我们直接简单粗暴地拆开
f(x)=(x-a)(x2-2bx+b2)=x3-(a+2b)x2+b(2a+b)x-ab2
按照套路来,我们求导
f'(x)=3x2-(2a+4b)x2+2ab+b2
不就是求零点吗?我们令f(x)以及f'(x)等于0就好了
令f(x)=0,那么x3-(a+2b)x2+b(2a+b)x-ab2=0
令f'(x)=0,那么f'(x)=3x2-(2a+4b)x2+2ab+b2
然后,就没有然后了
这里的f(x)我们千!万!不!要!拆!开!
f(x)=(x-a)(x-b)2
那么f(x)的零点显而易见是a和b
f'(x)=(x-b)2+(x-a)(2x-2b)【前导后不导加后导前不导】=(x-b)2+2(x-a)(x-b)=(x-b)(3x-2a-b)
x-b=0,x=b,3x-2a-b=0,x=(2a+b)/3
f'(x)的零点是b和(2a+b)/3
接下来我们就可以快乐地求a和b了
零点的集合是{-3,1,3}
说明{(2a+b)/3,a,b}={-3,1,3}
下面我们要使用的方法相信很多人在小学就会了,那就是猜
这里有一个技巧,先从复杂的开始猜
也就是先猜(2a+b)/3的值
①(2a+b)/3=-3
这种情况可以直接排除,因为剩下的a和b是两个正数,不可能正数加正数再乘以3就变成一个负数
②(2a+b)/3=1
这种情况也是可以的,2a+b=3,那么如果a取3,b取-3就刚刚好满足
③(2a+b)/3=3
这种情况不可以,2a+b不论a和b哪个取1或者-3都满足不了2a+b=9
所以我们可以求出,a=3,b=-3
此时,我们很自然地就可以写出f(x)=(x-3)(x+3)2,f'(x)=3(x+3)(x-1)
算到这一步,f(x)的极小值不是手到擒来?
f'(x)图像(灵魂画手上线):
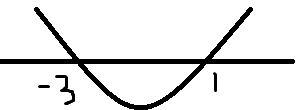
根据图像我们可以直观地看出f(x)的单调性(如果你想列表求单调性我不拦着你)
f(x)在(-∞,-3),(1,+∞)上单调递增,在(-3,1)上单调递减
众所周知,极小值在函数f(x)先减再增的地方,那么,此题最小值应该是在x=1的地方取到
把x=1带入f(x)可得f(1)=-32
(3)男人看了会沉默,女人看了会流泪的第三小题来了!
看第三小题,我们应该想一下,这个4/25是怎么来的,既然可以小于等于4/25,那么我们试试能不能找到这个特殊的点,也就是M=4/25
皇天不负有心人,因为0<b≤1,所以说明b=1肯定是一个特殊的值,我们把b=1带到f(x)试试
f(x)=x(x-1)²,f'(x)=(x-1)²+x(2x-2)【前导后不导加后导前不导】=(x-1)²+2x(x-1)=(x-1)(3x-1)
f'(x)图像(灵魂画手再次上线):
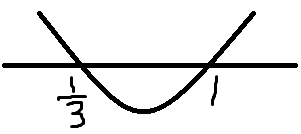
此时,极大值应该是x取1/3的地方取得
M=f(1/3)=4/27
OMG!4/27这个跟题目挂钩的值居然求出来了,既然4/27是x=1/3时f(x)的值,那么我们等一下肯定要把某个值和1/3扯上关系
刚才b的值我们带了1,现在b的值不确定,我们重新写一下f(x)和f'(x)
f(x)=(x²-x)(x-b)=x3-(b+1)x2+bx
f'(x)=3x²-2(b+1)x+bx
既然要求极大值,那么肯定要像第二小题那样求出f'(x)的零点
看到这么复杂的式子,我们先不要急着用求根公式或者因式分解求出具体的零点的值
我们设f'(x)的两个零点为x1和x2,并且x2>x1
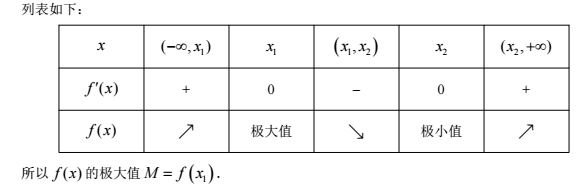
f'(x)的图像:
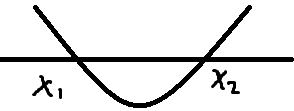
易知f(x1)是f(x)的最大值
M=f(x1)=x13-(b+1)x12+bx1
既然要证明M≤4/27,那么我们x13-(b+1)x12+bx1≤4/27
接下来我们继续减少未知数,我们找找b和x1之间的关系
别忘了x1不仅仅是f(x)的极大值点,同时x1也是f'(x)的一个零点
f'(x1)=0
3x12-2x1=2bx1-b
b(2x1-1)=3x12-2x1
b=(2x12-2x1)/(2x1-2)
把b带回M,可得M=x13-[(3x12-2x1)/(2x1-1)+1]x12+x1(2x12-2x1)/(2x1-2)=[x12(x1-1)]/(1-2x1)
接下来我们就可以求M的取值范围了,这里我们为了看得直观一点,我们换元
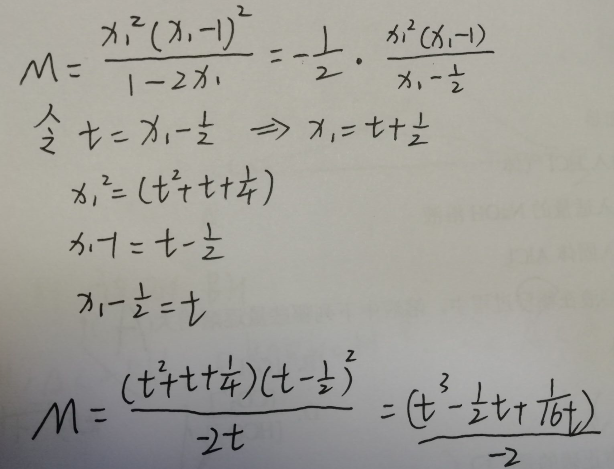
看到这里不要慌,有更加便捷的方式求M
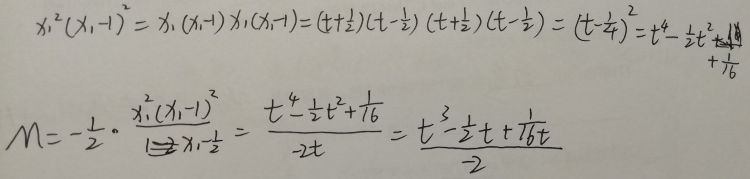
经过观察发现,分子可以拆成2个平方差公式
为了求M的取值范围,我们构造函数h(t)=t3-t/2+1/16t(暂时把-1/2抛开)
求导h'(t)=3t²-1/2-1/16t²,这里我们求一下t的取值范围
既然t=x1-1/2,那么我们就求一下x1的范围,x1跟b的关系在上面,如果用b=(2x12-2x1)/(2x1-2)来求x1的范围,肯定是不现实的(太麻烦了)

我们试一下能否通过图像来求出x1的范围
上面我们带过点了,当b=1的时候x1=1/3,那么b≠1的话我们再来看看x1和b的关系
前面我们知道x=1/3的时候是一个特殊点,这里我们带入试试f'(1/3)=(b-1)/3<0顺便带一下f'(0)=b>0,那么说明f'(x)的零点大于0,如图所示
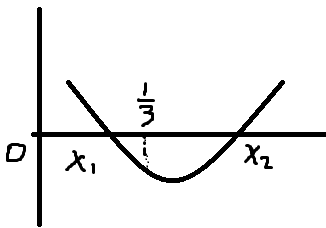
这说明了x1的范围应该是0<x1< 1/3
所以t的范围是-1/2<t<-1/6
t的范围求出来之后我们回到h'(t)=3t²-1/2-1/16t²,既然有个分母是未知数,我们就把整个式子写成分式,如图所示
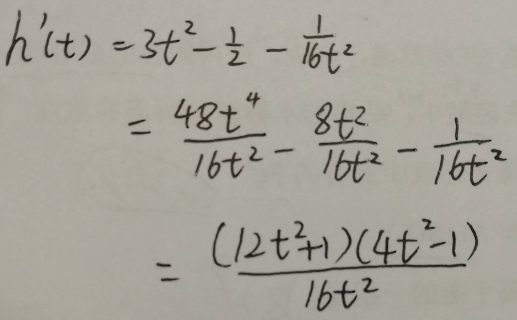
这里我们因式分解一下,如果不会因式分解就用求根公式求解,分母16t²和分子(16t²+1)恒大于0我们就不管了
我们看(4t²-1),由于t的范围是-1/2<t<-1/6,所以(4t²-1)<0,即h'(t)<0,h(t)在-1/2<t<-1/6上单调递减
那么h(-1/6)<h(t)<h(-1/2)
h(-1/6)=-8/27,h(-1/2)=0
到了这边,不要忘了,我们刚才把-1/2留在了M的位置,我们现在拿回来
M=h(t)×(-1/2)
所以0<M<4/27
再把b=1的特殊情况和b≠1的情况综合一下,0<M≤4/27
总结:第三小题的b先带特殊值1,然后求出了x=1/3时,M=4/27,接着我们有意识地把x1往1/3靠,最后通过一系列的换元,构造函数,求导解出最终答案
下面是规范解析:
小猿搜题版答案

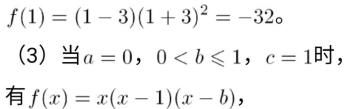



学校公布的答案




本文 暂无 评论