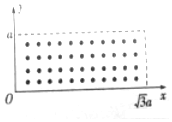
如图所示,在0≤x≤ 3 a、0≤y≤a范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为+q的带电粒子,它们的速度方向均在xOy平面的第一象限内,已知粒子在磁场中做圆周运动的周期为T,半径介于2a到3a之间,则下列说法正确的是( )
A.最后从磁场中飞出的粒子经历的时间为T/6
B.最后从磁场中飞出的粒子经历的时间大于T/6
C.最先从磁场上边界飞出的粒子经历的时间为T/12
D.最先从磁场上边界飞出的粒子经历的时间小于T/12
解析:
看到T肯定要先联想到求周期的公式,T=2πm/qB,由公式以及题意可知,所有发射的粒子周期是一样的
那么求时间我们列一下求时间的公式:t=θ/360°
看到ABCD四个选项,我们可以知道题目应该是要让我们把经历时间最长的粒子和经历时间最短的粒子求出来。
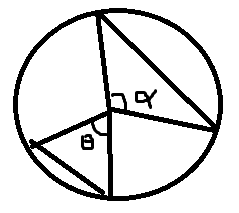
首先,我们需要知道的是,弦越长,粒子转过的角度就越大,从而在磁场中经历的时间就越长,相反,弦越短,粒子在磁场中经历的时间就越短。
画个图理解一下(灵魂画手上线)
其次,题目没说发出的粒子速度相同,因为r=mv/qB,所以我们这里还需要考虑一种情况,那就是当弦长一定的时候,半径对角度的影响(灵魂画手再次上线)
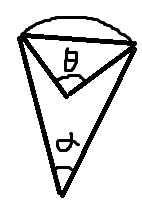
由图像可知,弦长一定时,半径越大,那么角度越小,反之,半径越小,角度越大。
那么我们要如果想求最大时间的话肯定是要半径最小,且弦长最长,如果要求最小时间的话就需要最大的半径,且最短的弦长
下图为最长的弦,因为磁场是有界磁场,且为长方形,所以长方形的斜边是最长的弦,因为题目给了半径范围2a到3a,所以说这里的半径为2a,用正弦定理就可以求出角度了
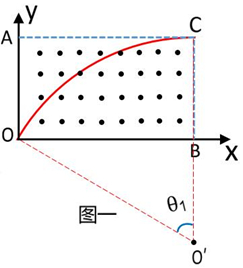
最短的弦就是长方形中较短的边,半径易得为3a,用正弦定理就可以求出角度了
答案:
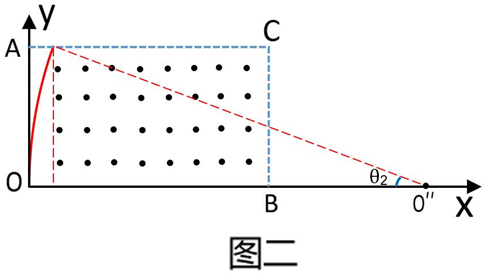
解:A、B、设磁场区域为OACB,根据周期公式T=2πm/qB可知粒子在磁场中运动的周期相同,分析可知最后从磁场中飞出的粒子轨迹如图一所示,此时粒子半径R1=2a,恰好在C点离开磁场,延长CB至O′使CO′=2a,O′即为圆心,连接OO′,根据几何关系可知,此时粒子转过圆心角θ1最大为60°,所以最后从磁场中飞出的粒子经历的时间为:t1=θ1/360°=60°/360°T=T/6,故A正确,B错误;C、D、分析可知最先从磁场上边界飞出的粒子运动轨迹如图二所示,此时粒子半径R2=3a,O′′为圆心,此时粒子转过圆心角θ2,根据几何关系可知,sinθ2=1/3<sin30°=1/2,所以可知θ2<30°,故最先从磁场上边界飞出的粒子经历的时间为:t2=θ2/360°T<30°/360°T=T12,故D正确,C错误。
故选:AD。


本文 暂无 评论