啊涛博客

已知函数f（x）=x-1-aln^x

（1）若f（x）≥0，求a的值；

（2）设m为整数，且对于任意正整数n，（1+2^-1）（1+2^-2）（1+2^-n）＜m，求m最小值。

第一题很明显先求导，然后判断这个函数的单调性

f'（x）=1-x^-a，令f'（x）=0，求出x=a

①a≤0，那么f'（x）恒大于0，f（x）在0到正无穷单调递增

f'（x）的图像

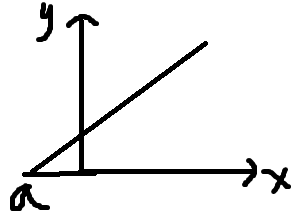
f（x）的图像

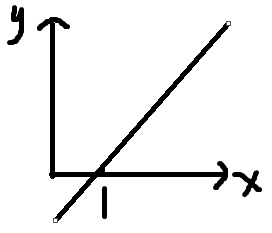
很明显，不符合题目的f（x）≥0

①a＞0.那么f'（x）在0到a之间小于0，a到正无穷大于0，所以f（x）在0到a之间单调递减，在a到正无穷单调递增

f'（x）的图像

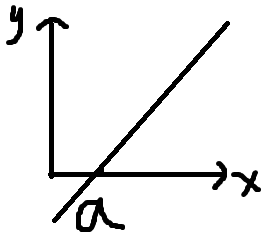
f（x）的图像

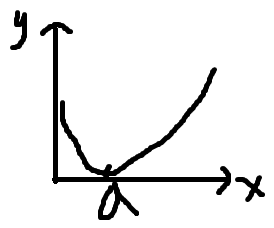
此时f（x）的最小值是f（a），因为题目说f（x）≥0，所以f（a）=0，又因为f（1）=0，所以a=1

（2）由（1）可知，当a=1时，f（x）=x-1-ln^x≥0，即ln^x≤x-1

可推出ln^x+1≤x，令x=1+2^-n得ln（1+2^-n）≤2^-n【想到这一步是因为第二小题给出（1+2^-1）（1+2^-2）（1+2^-n）这样的式子】

并且，此时不取等号了，因为此时（1+2^-n），必然大于1。所以，此时x必然大于1，因此取不到等号）

（看图加深理解）

（如果还不能理解那就换元，令t=1+2^-n＞1，所以f（t）＞0）

从而，ln（1+2^-1）+ln（1+2^-2）+……+ln（1+2^-n）＜2^-1+2^-2+2^-n=1-2^-n＜1

（可带数字检验，2^-1+2^-2+2^-3+2^-4=1-2^-4）

两边同时把ln去掉（ln^N=x，e^x=N）

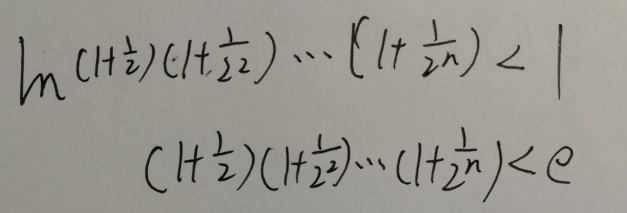
所以可以得到上图的式子，由于e≈2.718281828459

因为m是整数，所以，m的最小值是3。

打赏

微信QQ支付宝扫一扫，打赏作者吧～