已知函数f(x)=2x3-ax2+2
(1)讨论 f(x)的单调性
(2)当0<a<3时,记f(x)在区间[0,1]的最大值为M,最小值为m,求M-m的取值范围。
第一题肯定要先求导
f'(x)=6x2-2ax=2x(3x-a),△=4a2
令f'(x)=0,可求出x=0或x=a/3
①若a>0(此时△>0),则当x属于(-∞,0)和(a/3,+∞)时,f'(x)>0,x属于(0,a/3)时,f'(x)<0
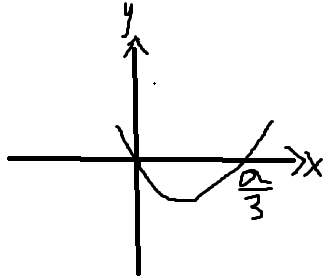
②若a=0(此时△=0),f'(x)在R上大于0
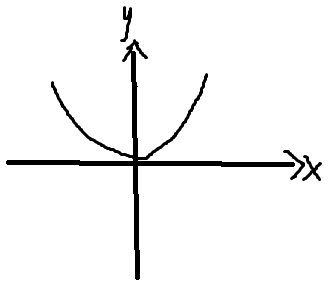
③若a<0(此时△>0),f'(x)在(-∞,a/3)和(0,+∞)大于0,f'(x)在(a/3,0)小于0

第一题其实给第二题作了铺垫
第二题0<a<3,属于第一题①的情况,易得f(x)在(0,a/3)上单调递减,在(a/3,1)上单调递增(此时x的取值范围是[0,1]所以不能写(a/3,+∞)上递增)
老规矩,先算一下端点的值,f(0)=2,f(1)=2-a+2=4-a>1
易知,f(x)的最小值应该是f(a/3)=-a3/27+2>1,m=-a3/27+2,最大值M为4-a或2

如果0<a<2,那么M是4-a
如果2≤a<3,那么M是2
所以
(1)M-m=2-a+a3/27,(0<a<2)
(2)M-m=a3/27,(2≤a<3)
接下来就很简单了,分别求出这两个式子的范围即可
(1)当0<a<2时,令h(a)=2-a+a3/27
h'(a)=a2/9-1<0(0<a<2),所以h(a)在0<a<2上单调递减,h(0)=2(取不到,就是意思意思算一下),h(2)=8/27(取不到,就是意思意思算一下)
所以,h(a)即(M-m)的取值范围是(8/27,2)
(2)当2≤a<3时,令t(a)=a3/27
t'(a)=a2/9>0(2≤a<3),所以t(a)在2≤a<3上单调递增,t(2)=8/27(取得到),t(3)=1(取不到,就是意思意思算一下)
所以,t(a)即(M-m)的取值范围是[8/27,2)
综上所述,M-m的取值范围是[8/27,2)


本文 暂无 评论