啊涛博客

已知点A，B关于坐标原点O对称，丨AB丨=4，圆M过点A，B且与直线x+2=0相切。

（1）若A在直线x+y=0上，求圆M的半径。

（2）是否存在定点P，使得当A运动时，丨MA丨-丨MP丨为定值？并说明理由。

解：

（1）遇到这种题，第一反应，画图

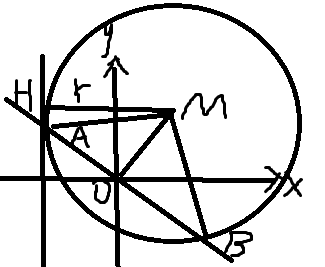
求半径肯定用用到半径的表达式，因为圆M和x=-2相切，设切点为H，所以丨MH丨=r

因为圆M过A，B点，所以圆心M必在AB的垂直平分线上，因为点A在直线x+y=0上，A，B关于坐标原点O对称，所以A，B都在x+y=0上

因此，M在x+y=0的垂直平分线，y-x=0上，设M（a，a）

所以丨MH丨=r=丨a+2丨

因为丨AB丨=4，所以丨AO丨=2，因为M（a，a），所以丨MO丨=√2a

根据垂径定理，∠MOA=90°

再根据勾股定理，丨MO丨²+丨AO丨²=丨MA丨²

4+2a²=（a+2）²

求出a=0或4，所以r=2或6

（2）第二题没说A，B具体在哪条直线，所以我们没办法知道M在哪条直线上，因此我们设M（x，y）

还是利用∠MOA=90°以及丨MO丨²+丨AO丨²=丨MA丨²，可列出：x²+y²+4=（x+2）²

可得，y²=4x，所以M点在抛物线上。

第二题要的是定点，很明显，抛物线的定点应该是焦点（1，0），我们试一下是不是焦点

如果P（1，0），那么丨MP丨=丨MN丨=x+1

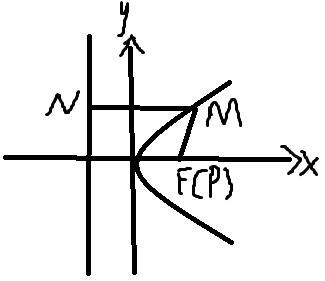
丨MA丨-丨MP丨=r-丨MP丨=x+2-（x+1）=1，果真符合题目要的定值，说明P点就是抛物线的焦点。

打赏

微信QQ支付宝扫一扫，打赏作者吧～