已知函数f(x)=ex(ex-a)-a2x
(1)讨论f(x)的单调性。
(2)若f(x)≥0,求a的取值范围。
解:
(1)讨论单调性肯定要求导,求导结果:f'(x)=2e2x-aex-a2=2(ex)2-aex-a2
这个时候不要着急令f'(x)=0(当然,如果你有能力算出f'(x)=0时x的值的话也行)。
我们观察这个式子可以发现,这个式子很像一个完全平方公式的展开项,我们把它配回去。
这里有2种方法,分别是十字相乘法和下面要讲的这种配凑的方法,由于篇幅问题这里就讲一种。
f'(x)=2(ex)2-aex-a2=2(ex)2-2aex+aex-a2=2ex(ex-a)+a(ex-a)=(2ex+a)(ex-a)。
很明显,这里我们需要讨论一下a的情况:
①a=0
那么f'(x)=2e2x,易知f'(x)>0。
f(x)在R上单调递增。
②a>0
此时(2ex+a)>0,我们只需要讨论(ex-a)的正负情况。
很明显,x=lna时,ex-a=0,那么f'(x)=0,这里如果要判断f'(x)的正负我们就需要判断x>lna以及x<lna时,ex-a的正负情况。
易知,(ex-a)为递增函数,所以,x>lna时,f'(x)>0,x<时,f'(x)<0。
f(x)在x>lna时,单调递增,f(x)在x<lna时,单调递减。
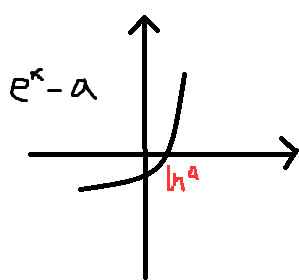
③a<0
此时(ex-a)>0,我们只需要讨论(2ex+a)的正负情况。
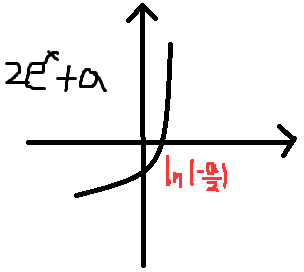
令2ex+a=0,可求出x=ln(-a/2),同样的,(2ex+a)也为增函数,所以x<ln(-a/2)时f'(x)<0,x>ln(-a/2)时,f'(x)>0
f(x)在x>ln(-a/2)时,单调递增,f(x)在x<ln(-a/2)时,单调递减。
(2)如果第一小题做出来了,第二小题应该是没有什么问题的。
题目说f(x)≥0,说明了什么?说明f(x)的最小值是0,只要你能使f(x)的最小值大于等于0就行了。
我们先把第一题讨论的3种情况的f(x)图像画一下。
①a=0(单调递增)

由于a=0,那么f(x)=e2x(直接就可以看出来大于0)
②a>0,f(x)在x>lna时,单调递增,f(x)在x<lna时,单调递减。
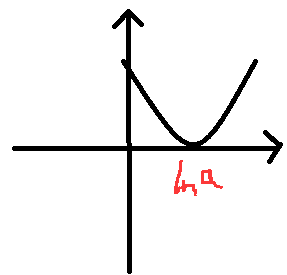
此时,f(x)的最小值为f(lna),那么使f(lna)≥0即可。
f(lna)=a(a-a)-a2×lna≥0,因为a>0,所以a2>0,两边同时除以-a2可得lna≤0,0<a≤1
③a<0,f(x)在x>ln(-a/2)时,单调递增,f(x)在x<ln(-a/2)时,单调递减。

此时,f(x)的最小值为f(ln(-a/2)),那么使(ln(-a/2))≥0即可。
f(ln(-a/2))=3a2/4-a2ln(-a/2)≥0,因为a<0,所以a2>0,两边同时除以a2可得ln(-a/2)≤3/4,-a≤2e3/4,0<a≥-2e3/4
综上所述,-2e3/4≤a≤1
下面献上规范的答案:




本文 暂无 评论