在直角坐标系xOy中,曲线y=x2+mx-2与x轴交与A,B两点,点C的坐标为(0,1)。
当m变化时,解决下面问题:
(1)能否出现AC⊥BC的情况?说明理由:
(2)证明过A,B,C,三点的圆在y轴上截得的弦长为定值。
解析:
(1)这种曲线题,先画图(对称轴:x=-m/2,不知道m的正负情况就假设m>0吧!)
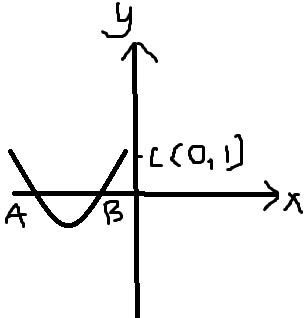
设A(x1,0)B(x2,0)
证明垂直的方法有很多,比如斜率相乘等于-1,向量相乘等于0,甚至勾股定理用上
鉴于这篇文章:http://www.atboke.cn/?id=37
我这里就拿向量相乘等于0来做这道题
向量AC=(-x1,1),向量BC=(-x2,1)
向量AC×向量BC=x1x2+1
聪明如你,肯定一眼看出来此处需要韦达定理
A和B都是y=x2+mx-2上的点,因为题中很明确y=x2+mx-2与x轴交于A,B两点,那么△>0,所以可以用韦达定理(△≥0是使用伟达定理的前提)
因此,x1x2=-2,向量AC×向量BC=x1x2+1=-1≠0,不能出现AC⊥BC的情况(同时向量相乘小于0,我们就可以知道AC和BC夹角大于90°)
(2)继续画图
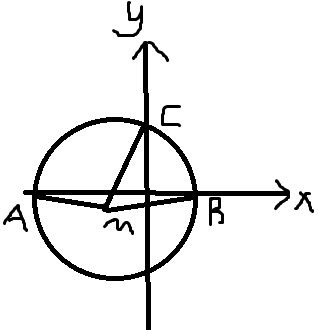
过A,B,C三点的圆的圆心必定在线段AB的垂直平方线上,那么我们就可以知道圆心的横坐标是(x1+x2)/2=-m/2
设圆心M的坐标为(-m/2,y0)
题目似乎没有给其他条件了,那么我们就想一下圆有哪些性质
与此同时我们还需要把y0用某个式子表达一下,思来想去也只有垂径定理了
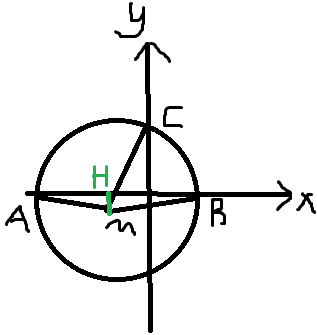
丨AM丨²=丨MH丨²+丨AH丨²
丨AM丨²=y02+(-m/2-x1)2
丨MH丨²=y02
丨AH丨²=(-m/2-x1)²
我们发现,这个时候等式左右居然消得干干净净!
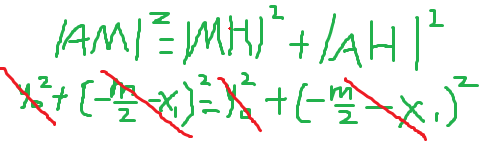
因为半径跟半径是相等的,所以丨AM丨=丨MC丨=丨MB丨
因为C点的坐标已知,我们就用丨MC丨替换丨AM丨
丨MC丨²=(y0-1)2+(-m/2-0)2
最后我们可以得出y0=-1/2
所以M点的坐标为(-m/2,-1/2)
所以圆的方程为:
(x+m/2)²+(y+1/2)²=(-m/2)²+(-1/2-1)²=丨MC丨²
题目要求我们证明过A,B,C,三点的圆在y轴上截得的弦长为定值。那么就说明我们要证明图中粉红色线段长度为定值
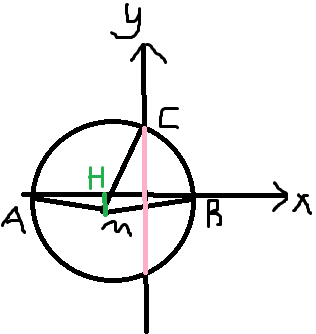
令x=0得y1=1,y2=-2,所以这条粉红色的长度为y1-y2=3
下面是规范解析:



本文 暂无 评论