
解析:
(1)老规矩,遇到图形题先画图
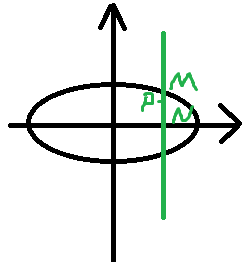
求P点轨迹方程我们就设P点的坐标为(x,y),M(x0,y0),N(x0,0)
此时向量NP=(x-x0,y)向量NM=(0,y0)
根据题目所给的条件,可以列出:x-x0=0,y=√2y0
因为M点在椭圆上,把P点的坐标用x0和y0表示,然后带入椭圆方程即可得出P点的轨迹方程为x²+y²=2
(2)
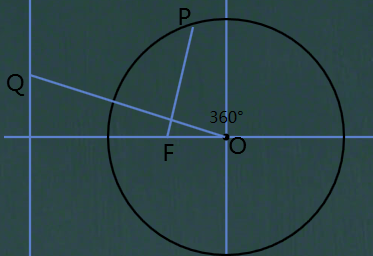
题目要我们证明PF⊥OQ,那么我们看看如果PF⊥OQ的话,PF和OQ满足什么关系
我们设P(m,n),Q(-3,t)
因为F是椭圆的左焦点,易得F(-1,0)
向量PF=(-1-m,-n),向量OQ=(3,-t)
向量PF×向量OQ=-3-3m+tn=0
那么我们要证明PF⊥OQ我们就必须证明-3-3m+tn=0
题目给我们一个条件向量OP×向量PQ=1,向量OP=(m,n)向量PQ=(-3-m,t-n),可以列出以下式子:
-3m-m²+tn-n²=1,由(1)可得m²+n²=2,所以-3m+tn=3,因此-3-3m+tn=0等式成立
本文标题:数学2017年文科全国2卷第20题解析
本文链接:https://atboke.cn/?id=56
版权声明:本文不使用任何协议授权,您可以任何形式自由转载或使用。


本文 暂无 评论